1. Rigid Body Motion: Rigid Body Transformation

Rigid Body and Rigid Motion

The motion of a partical moving in Euclidean space is described by giving the location of the partical at each instant of time. A trajectory of the particle is represented by the parameterized curve $p(t) = (x(t), y(t), z(t)) \in \mathbb{R}^3$.

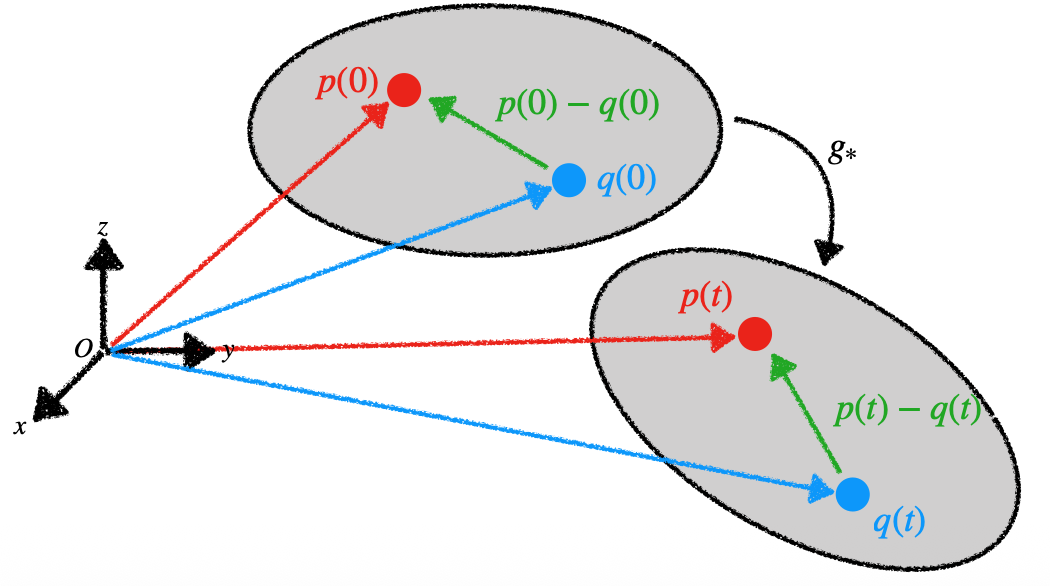
However, in robotics, we are interested in collective motion of a set of particles. We thus define rigid body as a collection of particles such that the distance between any two particles remains fixed. That is, for any point $p(t)$ and $q(t)$ on rigid body on time $t$,

A rigid motion is then the continuous movement of the particles in the object that preserves the distance between any particles on the object.

Rigid Body Transformation

Preserving only distance may not preserve orientation (e.g., $(x, y, z) \rightarrow (x, y, -z)$). To remove this possibility, we require that the cross product between vectors in the body also be preserved. Formally, A mapping $g: \mathbb{R}^3 \rightarrow \mathbb{R}^3$ is a rigid body transformation if

1. Distance preservation: For all points $p, q \in \mathbb{R}^3$,

   \[\lVert g(p) - g(q) \rVert = \lVert p - q \rVert\]

2. Cross product preservation: For all vectors $v, w \in \mathbb{R}^3$,

   \[g_*(v \times w) = g_*(v) \times g_* (w)\]

   where $g_*(v) = g(p’) - g(q’)$ if $p’, q’$ are some points (transformation on vectors).

Here, the important thing is that the cross product of vector is preserved, not the point (this will be dealt later).

Interesting Property

Fact: from the above definition, the inner product of two vectors is also preserved in the rigid body transformation.

Proof: Using polarization identity,

\(v_1^Tv_2 = \cfrac{1}{4}(\lVert v_1 + v_2 \rVert^2 - \lVert v_1 - v_2\rVert^2)\) and the fact that

\(\lVert v_1 + v_2 \rVert = \lVert g_*(v_1) + g_*(v_2) \rVert, \quad \lVert v_1 - v_2 \rVert = \lVert g_*(v_1) - g_*(v_2) \rVert\) to conclude that for any two vectors $v_1$, $v_2$,